2°3 Vespertino_Actividad_14MAYO2020

Buenas Tardes segundo tres turno vespertino

Alumnos que no entregaron la actividad del 11 de mayo o su correo no a llegado

Fernández García, Gallegos Solano, Hernández Bello, Martínez Jiménez, Moncada Cornejo,

Rangel Guzmán, Trejo Castro y Yáñez Trujillo 

Antes de resolver su ejercicio revisen bien el que esta propuesto

En este ejemplo tomaremos la función del tipo f(x) =   √ (ax² + bx + c)

Ejemplo 1.- Dada la función f(x) = √ (x² – 7x + 12)   Determinar el punto de inicio de la gráfica, dominio, rango indica el intervalo donde la función es creciente o decreciente, continua o discontinua, par o impar Representar gráficamente la función.

Solución:

Primero tomamos la expresión que se encuentra dentro de la raíz y lo igualamos a cero

  X² – 7x + 12 = 0 Factorizamos (x – 4) (x – 3)    cada factor lo igualamos a cero

   x – 4 = 0 entonces x = 4   

   x – 3 = 0 entonces x = 3  

Hay dos valores para la función 3, 4 lugares donde la gráfica inicia

Tomamos un valor cualquiera a la izquierda del 3 ejemplo –1 y lo evaluamos en la función original

 √ {(–1)² – 7(–1) + 12}      √ (1 + 7 + 12)   à  √20   =   4.5

Por lo tanto, tenemos un punto por donde la gráfica pasa (–1. 4.5)

Ahora tomamos cualquier valor a la derecha del 4 ejemplo 6 y lo evaluamos en la función original

  √ {(6)² – 7(6) + 12}      √ (36 – 42 + 12)   à  √6   = 2.5

Por lo tanto, tenemos un punto por donde la gráfica pasa (6, 2.5),

ubicamos los 4 valores en el eje x como esta en la gráfica –1, 3, 4 y 6 

Graficamos los puntos y la gráfica queda de la siguiente forma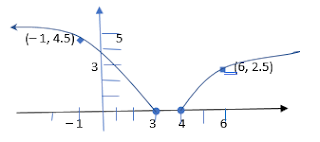

Dominio (– ∞, 3] u [4, ∞)              Rango [0, ∞)

Función Discontinua, función par, función Decreciente (– ∞, 3] función Creciente [4. ∞)

Ejercicio Dada la función f(x) = √ (x² + 8x + 12)   Determinar el punto de inicio de la gráfica, dominio, rango indica el intervalo donde la función es creciente o decreciente, continua o discontinua, par o impar Representar gráficamente la función.